Answer Keys > Chapter 4
|
Published in 1991 by Wellesley-Cambridge Press, the book is a useful resource for educators and self-learners alike. It is well organized, covers single variable and multivariable calculus in depth, and is rich with applications. There is also an online Instructor's Manual and a student Study Guide.
- In part (b) the student only finds two of the three values, so the first point was not earned. The justification point was not earned because it is not true that f ′ changes from increasing to decreasing at x =−1. In part (d) the student earned the first 2 points since x =1 is identified as a candidate and the endpoints are considered.
- Enrolling in AP Calculus comes with the understanding that you will take the AP exam in May. The 2019 test will be given May 5, 2020. If you do not plan on taking the AP Exam, we must have a conversation about it first. My goal is for each of you to receive credit by passing the AP Exam. That means we strive for a five!!!
- This is the additional review for the first part of chapter 4. (The second of the 3 reviews).
The complete textbook is also available as a single file. (PDF - 38.5MB)
Highlights of Calculus MIT Professor Gilbert Strang has created a series of videos to show ways in which calculus is important in our lives. The videos, which include real-life examples to illustrate the concepts, are ideal for high school students, college students, and anyone interested in learning the basics of calculus. › Watch the videos |
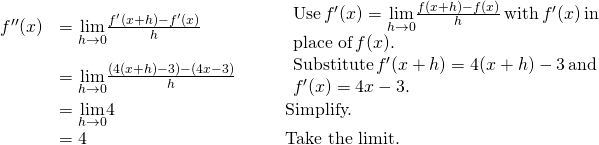
4.4 Analytical Connections f, f', f' (part 1) Video Notes 2nd Derivative Sign Diagram Ex 3 (day 2) Video Notes 2nd Derivative Test (day 2). View Homework Help - MathAssessmentSolutions.pdf from ECON 301 at Rutgers University. Calculus Assessment Test for Intermediate Microeconomics - Solutions Question 1.
Textbook Components
- Table of Contents (PDF)
- Answers to Odd-Numbered Problems (PDF - 2.4MB)
- Equations (PDF)
| ChapterS | FILES |
|---|---|
| 1: Introduction to Calculus, pp. 1-43 1.1 Velocity and Distance, pp. 1-7 1.2 Calculus Without Limits, pp. 8-15 1.3 The Velocity at an Instant, pp. 16-21 1.4 Circular Motion, pp. 22-28 1.5 A Review of Trigonometry, pp. 29-33 1.6 A Thousand Points of Light, pp. 34-35 1.7 Computing in Calculus, pp. 36-43 | Chapter 1 - complete (PDF - 2.2MB) Chapter 1 - sections: 1.1 - 1.4 (PDF - 1.6MB) |
| 2: Derivatives, pp. 44-90 2.1 The Derivative of a Function, pp. 44-49 2.2 Powers and Polynomials, pp. 50-57 2.3 The Slope and the Tangent Line, pp. 58-63 2.4 Derivative of the Sine and Cosine, pp. 64-70 2.5 The Product and Quotient and Power Rules, pp. 71-77 2.6 Limits, pp. 78-84 2.7 Continuous Functions, pp. 85-90 | Chapter 2 - complete (PDF - 3.8MB) Chapter 2 - sections: 2.1 - 2.4 (PDF - 2.3MB) |
| 3: Applications of the Derivative, pp. 91-153 3.1 Linear Approximation, pp. 91-95 3.2 Maximum and Minimum Problems, pp. 96-104 3.3 Second Derivatives: Minimum vs. Maximum, pp. 105-111 3.4 Graphs, pp. 112-120 3.5 Ellipses, Parabolas, and Hyperbolas, pp. 121-129 3.6 Iterations x[n+1] = F(x[n]), pp. 130-136 3.7 Newton's Method and Chaos, pp. 137-145 3.8 The Mean Value Theorem and l'Hôpital's Rule, pp. 146-153 | Chapter 3 - complete (PDF - 3.3MB) Chapter 3 - sections: 3.1 - 3.4 (PDF - 1.5MB) |
| 4: The Chain Rule, pp. 154-176 4.1 Derivatives by the Charin Rule, pp. 154-159 4.2 Implicit Differentiation and Related Rates, pp. 160-163 4.3 Inverse Functions and Their Derivatives, pp. 164-170 4.4 Inverses of Trigonometric Functions, pp. 171-176 | Chapter 4 - complete (PDF - 1.1MB) Chapter 4 - sections: 4.1 - 4.2 (PDF) |
| 5: Integrals, pp. 177-227 5.1 The Idea of an Integral, pp. 177-181 5.2 Antiderivatives, pp. 182-186 5.3 Summation vs. Integration, pp. 187-194 5.4 Indefinite Integrals and Substitutions, pp. 195-200 5.5 The Definite Integral, pp. 201-205 5.6 Properties of the Integral and the Average Value, pp. 206-212 5.7 The Fundamental Theorem and Its Consequences, pp. 213-219 5.8 Numerical Integration, pp. 220-227 | Chapter 5 - complete (PDF - 3.3MB) Chapter 5 - sections: 5.1 - 5.4 (PDF - 1.1MB) |
| 6: Exponentials and Logarithms, pp. 228-282 6.1 An Overview, pp. 228-235 6.2 The Exponential e^x, pp. 236-241 6.3 Growth and Decay in Science and Economics, pp. 242-251 6.4 Logarithms, pp. 252-258 6.5 Separable Equations Including the Logistic Equation, pp. 259-266 6.6 Powers Instead of Exponentials, pp. 267-276 6.7 Hyperbolic Functions, pp. 277-282 | Chapter 6 - complete (PDF - 3.1MB) Chapter 6 - sections: 6.1 - 6.4 (PDF - 2.1MB) |
| 7: Techniques of Integration, pp. 283-310 7.1 Integration by Parts, pp. 283-287 7.2 Trigonometric Integrals, pp. 288-293 7.3 Trigonometric Substitutions, pp. 294-299 7.4 Partial Fractions, pp. 300-304 7.5 Improper Integrals, pp. 305-310 | Chapter 7 - complete (PDF - 1.7MB) Chapter 7 - sections: 7.1 - 7.3 (PDF - 1.2MB) |
| 8: Applications of the Integral, pp. 311-347 8.1 Areas and Volumes by Slices, pp. 311-319 8.2 Length of a Plane Curve, pp. 320-324 8.3 Area of a Surface of Revolution, pp. 325-327 8.4 Probability and Calculus, pp. 328-335 8.5 Masses and Moments, pp. 336-341 8.6 Force, Work, and Energy, pp. 342-347 | Chapter 8 - complete (PDF - 2.1MB) Chapter 8 - sections: 8.1 - 8.3 (PDF - 1.1MB) |
| 9: Polar Coordinates and Complex Numbers, pp. 348-367 9.1 Polar Coordinates, pp. 348-350 9.2 Polar Equations and Graphs, pp. 351-355 9.3 Slope, Length, and Area for Polar Curves, pp. 356-359 9.4 Complex Numbers, pp. 360-367 | Chapter 9 - complete (PDF) Chapter 9 - sections: 9.1 - 9.2 (PDF) |
| 10: Infinite Series, pp. 368-391 10.1 The Geometric Series, pp. 368-373 10.2 Convergence Tests: Positive Series, pp. 374-380 10.3 Convergence Tests: All Series, pp. 325-327 10.4 The Taylor Series for e^x, sin x, and cos x, pp. 385-390 10.5 Power Series, pp. 391-397 | Chapter 10 - complete (PDF - 2.0MB) Chapter 10 - sections: 10.1 - 10.3 (PDF - 1.3MB) |
| 11: Vectors and Matrices, pp. 398-445 11.1 Vectors and Dot Products, pp. 398-406 11.2 Planes and Projections, pp. 407-415 11.3 Cross Products and Determinants, pp. 416-424 11.4 Matrices and Linear Equations, pp. 425-434 11.5 Linear Algebra in Three Dimensions, pp. 435-445 | Chapter 11 - complete (PDF - 3.3MB) Chapter 11 - sections: 11.1 - 11.3 (PDF - 2.2MB) |
| 12: Motion along a Curve, pp. 446-471 12.1 The Position Vector, pp. 446-452 12.2 Plane Motion: Projectiles and Cycloids, pp. 453-458 12.3 Tangent Vector and Normal Vector, pp. 459-463 12.4 Polar Coordinates and Planetary Motion, pp. 464-471 | Chapter 12 - complete (PDF - 1.2MB) Chapter 12 - sections: 12.1 - 12.2 (PDF) |
| 13: Partial Derivatives, pp. 472-520 13.1 Surface and Level Curves, pp. 472-474 13.2 Partial Derivatives, pp. 475-479 13.3 Tangent Planes and Linear Approximations, pp. 480-489 13.4 Directional Derivatives and Gradients, pp. 490-496 13.5 The Chain Rule, pp. 497-503 13.6 Maxima, Minima, and Saddle Points, pp. 504-513 13.7 Constraints and Lagrange Multipliers, pp. 514-520 | Chapter 13 - complete (PDF - 3.9MB) Chapter 13 - sections: 13.1 - 13.4 (PDF - 2.3MB) |
| 14: Multiple Integrals, pp. 521-548 14.1 Double Integrals, pp. 521-526 14.2 Changing to Better Coordinates, pp. 527-535 14.3 Triple Integrals, pp. 536-540 14.4 Cylindrical and Spherical Coordinates, pp. 541-548 | Chapter 14 - complete (PDF - 1.9MB) Chapter 14 - sections: 14.1 - 14.2 (PDF - 1.0MB) |
| 15: Vector Calculus, pp. 549-598 15.1 Vector Fields, pp. 549-554 15.2 Line Integrals, pp. 555-562 15.3 Green's Theorem, pp. 563-572 15.4 Surface Integrals, pp. 573-581 15.5 The Divergence Theorem, pp. 582-588 15.6 Stokes' Theorem and the Curl of F, pp. 589-598 | Chapter 15 - complete (PDF - 3.1MB) Chapter 15 - sections: 15.1 - 15.3 (PDF - 1.5MB) |
| 16: Mathematics after Calculus, pp. 599-615 16.1 Linear Algebra, pp. 599-602 16.2 Differential Equations, pp. 603-610 16.3 Discrete Mathematics, pp. 611-615 | Chapter 16 - complete (PDF) Chapter 16 - sections: 16.1 - 16.2 (PDF) |
Welcome!
This OCW supplemental resource provides material from outside the official MIT curriculum.
MIT OpenCourseWare is a free & open publication of material from thousands of MIT courses, covering the entire MIT curriculum.
No enrollment or registration. Freely browse and use OCW materials at your own pace. There's no signup, and no start or end dates.
Knowledge is your reward. Use OCW to guide your own life-long learning, or to teach others. We don't offer credit or certification for using OCW.
4.4 Analytical Connections f, f', f' (part 1) Video Notes 2nd Derivative Sign Diagram Ex 3 (day 2) Video Notes 2nd Derivative Test (day 2). View Homework Help - MathAssessmentSolutions.pdf from ECON 301 at Rutgers University. Calculus Assessment Test for Intermediate Microeconomics - Solutions Question 1.
Textbook Components
- Table of Contents (PDF)
- Answers to Odd-Numbered Problems (PDF - 2.4MB)
- Equations (PDF)
| ChapterS | FILES |
|---|---|
| 1: Introduction to Calculus, pp. 1-43 1.1 Velocity and Distance, pp. 1-7 1.2 Calculus Without Limits, pp. 8-15 1.3 The Velocity at an Instant, pp. 16-21 1.4 Circular Motion, pp. 22-28 1.5 A Review of Trigonometry, pp. 29-33 1.6 A Thousand Points of Light, pp. 34-35 1.7 Computing in Calculus, pp. 36-43 | Chapter 1 - complete (PDF - 2.2MB) Chapter 1 - sections: 1.1 - 1.4 (PDF - 1.6MB) |
| 2: Derivatives, pp. 44-90 2.1 The Derivative of a Function, pp. 44-49 2.2 Powers and Polynomials, pp. 50-57 2.3 The Slope and the Tangent Line, pp. 58-63 2.4 Derivative of the Sine and Cosine, pp. 64-70 2.5 The Product and Quotient and Power Rules, pp. 71-77 2.6 Limits, pp. 78-84 2.7 Continuous Functions, pp. 85-90 | Chapter 2 - complete (PDF - 3.8MB) Chapter 2 - sections: 2.1 - 2.4 (PDF - 2.3MB) |
| 3: Applications of the Derivative, pp. 91-153 3.1 Linear Approximation, pp. 91-95 3.2 Maximum and Minimum Problems, pp. 96-104 3.3 Second Derivatives: Minimum vs. Maximum, pp. 105-111 3.4 Graphs, pp. 112-120 3.5 Ellipses, Parabolas, and Hyperbolas, pp. 121-129 3.6 Iterations x[n+1] = F(x[n]), pp. 130-136 3.7 Newton's Method and Chaos, pp. 137-145 3.8 The Mean Value Theorem and l'Hôpital's Rule, pp. 146-153 | Chapter 3 - complete (PDF - 3.3MB) Chapter 3 - sections: 3.1 - 3.4 (PDF - 1.5MB) |
| 4: The Chain Rule, pp. 154-176 4.1 Derivatives by the Charin Rule, pp. 154-159 4.2 Implicit Differentiation and Related Rates, pp. 160-163 4.3 Inverse Functions and Their Derivatives, pp. 164-170 4.4 Inverses of Trigonometric Functions, pp. 171-176 | Chapter 4 - complete (PDF - 1.1MB) Chapter 4 - sections: 4.1 - 4.2 (PDF) |
| 5: Integrals, pp. 177-227 5.1 The Idea of an Integral, pp. 177-181 5.2 Antiderivatives, pp. 182-186 5.3 Summation vs. Integration, pp. 187-194 5.4 Indefinite Integrals and Substitutions, pp. 195-200 5.5 The Definite Integral, pp. 201-205 5.6 Properties of the Integral and the Average Value, pp. 206-212 5.7 The Fundamental Theorem and Its Consequences, pp. 213-219 5.8 Numerical Integration, pp. 220-227 | Chapter 5 - complete (PDF - 3.3MB) Chapter 5 - sections: 5.1 - 5.4 (PDF - 1.1MB) |
| 6: Exponentials and Logarithms, pp. 228-282 6.1 An Overview, pp. 228-235 6.2 The Exponential e^x, pp. 236-241 6.3 Growth and Decay in Science and Economics, pp. 242-251 6.4 Logarithms, pp. 252-258 6.5 Separable Equations Including the Logistic Equation, pp. 259-266 6.6 Powers Instead of Exponentials, pp. 267-276 6.7 Hyperbolic Functions, pp. 277-282 | Chapter 6 - complete (PDF - 3.1MB) Chapter 6 - sections: 6.1 - 6.4 (PDF - 2.1MB) |
| 7: Techniques of Integration, pp. 283-310 7.1 Integration by Parts, pp. 283-287 7.2 Trigonometric Integrals, pp. 288-293 7.3 Trigonometric Substitutions, pp. 294-299 7.4 Partial Fractions, pp. 300-304 7.5 Improper Integrals, pp. 305-310 | Chapter 7 - complete (PDF - 1.7MB) Chapter 7 - sections: 7.1 - 7.3 (PDF - 1.2MB) |
| 8: Applications of the Integral, pp. 311-347 8.1 Areas and Volumes by Slices, pp. 311-319 8.2 Length of a Plane Curve, pp. 320-324 8.3 Area of a Surface of Revolution, pp. 325-327 8.4 Probability and Calculus, pp. 328-335 8.5 Masses and Moments, pp. 336-341 8.6 Force, Work, and Energy, pp. 342-347 | Chapter 8 - complete (PDF - 2.1MB) Chapter 8 - sections: 8.1 - 8.3 (PDF - 1.1MB) |
| 9: Polar Coordinates and Complex Numbers, pp. 348-367 9.1 Polar Coordinates, pp. 348-350 9.2 Polar Equations and Graphs, pp. 351-355 9.3 Slope, Length, and Area for Polar Curves, pp. 356-359 9.4 Complex Numbers, pp. 360-367 | Chapter 9 - complete (PDF) Chapter 9 - sections: 9.1 - 9.2 (PDF) |
| 10: Infinite Series, pp. 368-391 10.1 The Geometric Series, pp. 368-373 10.2 Convergence Tests: Positive Series, pp. 374-380 10.3 Convergence Tests: All Series, pp. 325-327 10.4 The Taylor Series for e^x, sin x, and cos x, pp. 385-390 10.5 Power Series, pp. 391-397 | Chapter 10 - complete (PDF - 2.0MB) Chapter 10 - sections: 10.1 - 10.3 (PDF - 1.3MB) |
| 11: Vectors and Matrices, pp. 398-445 11.1 Vectors and Dot Products, pp. 398-406 11.2 Planes and Projections, pp. 407-415 11.3 Cross Products and Determinants, pp. 416-424 11.4 Matrices and Linear Equations, pp. 425-434 11.5 Linear Algebra in Three Dimensions, pp. 435-445 | Chapter 11 - complete (PDF - 3.3MB) Chapter 11 - sections: 11.1 - 11.3 (PDF - 2.2MB) |
| 12: Motion along a Curve, pp. 446-471 12.1 The Position Vector, pp. 446-452 12.2 Plane Motion: Projectiles and Cycloids, pp. 453-458 12.3 Tangent Vector and Normal Vector, pp. 459-463 12.4 Polar Coordinates and Planetary Motion, pp. 464-471 | Chapter 12 - complete (PDF - 1.2MB) Chapter 12 - sections: 12.1 - 12.2 (PDF) |
| 13: Partial Derivatives, pp. 472-520 13.1 Surface and Level Curves, pp. 472-474 13.2 Partial Derivatives, pp. 475-479 13.3 Tangent Planes and Linear Approximations, pp. 480-489 13.4 Directional Derivatives and Gradients, pp. 490-496 13.5 The Chain Rule, pp. 497-503 13.6 Maxima, Minima, and Saddle Points, pp. 504-513 13.7 Constraints and Lagrange Multipliers, pp. 514-520 | Chapter 13 - complete (PDF - 3.9MB) Chapter 13 - sections: 13.1 - 13.4 (PDF - 2.3MB) |
| 14: Multiple Integrals, pp. 521-548 14.1 Double Integrals, pp. 521-526 14.2 Changing to Better Coordinates, pp. 527-535 14.3 Triple Integrals, pp. 536-540 14.4 Cylindrical and Spherical Coordinates, pp. 541-548 | Chapter 14 - complete (PDF - 1.9MB) Chapter 14 - sections: 14.1 - 14.2 (PDF - 1.0MB) |
| 15: Vector Calculus, pp. 549-598 15.1 Vector Fields, pp. 549-554 15.2 Line Integrals, pp. 555-562 15.3 Green's Theorem, pp. 563-572 15.4 Surface Integrals, pp. 573-581 15.5 The Divergence Theorem, pp. 582-588 15.6 Stokes' Theorem and the Curl of F, pp. 589-598 | Chapter 15 - complete (PDF - 3.1MB) Chapter 15 - sections: 15.1 - 15.3 (PDF - 1.5MB) |
| 16: Mathematics after Calculus, pp. 599-615 16.1 Linear Algebra, pp. 599-602 16.2 Differential Equations, pp. 603-610 16.3 Discrete Mathematics, pp. 611-615 | Chapter 16 - complete (PDF) Chapter 16 - sections: 16.1 - 16.2 (PDF) |
Welcome!
This OCW supplemental resource provides material from outside the official MIT curriculum.
MIT OpenCourseWare is a free & open publication of material from thousands of MIT courses, covering the entire MIT curriculum.
No enrollment or registration. Freely browse and use OCW materials at your own pace. There's no signup, and no start or end dates.
Knowledge is your reward. Use OCW to guide your own life-long learning, or to teach others. We don't offer credit or certification for using OCW.
Made for sharing. Download files for later. Send to friends and colleagues. Modify, remix, and reuse (just remember to cite OCW as the source.)
4.4 Analytical Connections F F' F' (part 1)ap Calculus 14th Edition
Learn more at Get Started with MIT OpenCourseWare
